At What Nominal Rate Compounded Continuously Must Money Be Invested to Double in 4 Years

2.1 Exponential and Logarithmic Function Applications

Pre-Class:

• Take notes on the videos and readings (use the space below).
• Work and check problem #1 in the 2.1 NOTES section.
• Complete the 2.1 Pre-Class Quiz.

Introduction

Exponential functions occur frequently in science and business and are commonly used in compound interest applications.

• The value of a \$1000 investment returning 8% interest compounded monthly after 12 years would be calculated using the formula $$A=P\left(1+\frac rn\right)^{nt},$$

  where:

• A is the final amount in the account.
• P is the principal.
• r is the interest rate.
• n is the number of compounding periods per year.
• t is the number of years.


• The compounding frequency has a significant impact on the final amount of money (either saved or owed).

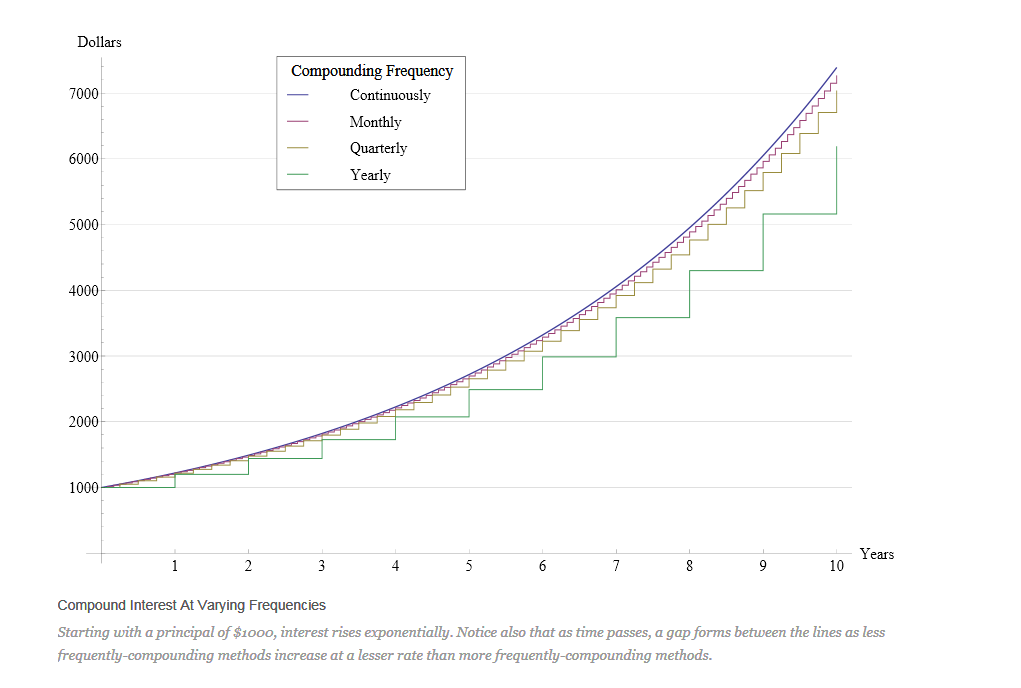
Notes

Compounding Frequency

• Yearly: $$A=1000(1+\frac{.08}1)^1=1080$$
• Quarterly: $$A=1000(1+\frac{.08}4)^4=1082.43$$
• Monthly: $$A=1000(1+\frac{.08}{12})^{12}=1083$$
• Daily: $$A=1000(1+\frac{.08}{365})^{365}=1083.28$$
• Continuously (at every instant): $$A=1000 \cdot~\underset{n\to \infty }{\mathop{\lim }}\,{{\left( 1+\frac{.08}{n} \right)}^{n}} =1083.29$$

Our focus will be on continuous compounding:

• What is e?
• Irrational number (similar to $\pi $ )
• 2.718281828459…..
• Like $\pi $, e occurs frequently in natural phenomena
  • Growth of bacterial cultures
  • Decay of a radioactive substance
• Formal definition of e: $$e=~\underset{n\to \infty }{\mathop{\lim }}\,{{\left( 1+\frac{1}{n} \right)}^{n}}$$ $$\approx ~~2.718281829$$

---

Notes

Continuous Compounding Formula (appreciation and depreciation): $$A = P{e^{rt}}$$

CONTINUOUS COMPOUND INTEREST: Round all answers to two decimal places.

1. Hometown Bank offers a CD that earns 1.58% compounded continuously. If \$10,000 is invested in this CD, how much will it be worth in 3 years?

   $A = 10,000{e^{.0158(3)}}$

   $A = \$ 10,485.41$

   The account will be worth approximately \$$10,485.41$ in three years.

2. Hometown Bank offers a CD that earns 1.58% compounded continuously. If \$10,000 is invested in this CD, how long will it take the account to be worth $11,000?

   $11,000 = 10,000{e^{.0158t}}$

   $\frac{{11,000}}{{10,000}} = \frac{{10,000{e^{.0158t}}}}{{10,000}}$

   $\frac{{11}}{{10}} = {e^{.0158t}}$

   $\ln \frac{{11}}{{10}} = \ln {e^{.0158t}}$

   $\ln \frac{{11}}{{10}} = .0158t$

   $\frac{{\ln \frac{{11}}{{10}}}}{{.0158}} = \frac{{.0158t}}{{.0158}}$

   $6.03 = t$

   It will take approximately 6.03 years for the account to be worth $11,000.

3. Doubling Time: How long will it take money to double if it is invested at 5% compounded continuously?

   $A = P{e^{rt}}$

   $2 = 1{e^{.05t}}$

   $2 = {e^{0.05t}}$

   $\ln 2 = \ln {e^{0.05t}}$

   $\ln 2 = 0.05t$

   $\frac{{\ln 2}}{{0.05}} = t$

   $t = 13.86$

   It will take approximately 13.86 years for the initial investment to double.

4. Doubling Rate: At what nominal rate compounded continuously must money be invested to double in 8 years?

   $A = P{e^{rt}}$

   $2 = 1{e^{r(8)}}$

   $2 = {e^{8r}}$

   $\ln 2 = \ln {e^{8r}}$

   $\ln 2 = 8r$

   $\frac{{\ln 2}}{8} = r$

   $0.0866 = r$

   In order for the initial investment to double in 8 years, the money must be invested in an account with a nominal rate of approximately 8.7% compounded continuously.

5. How long will it take money to triple if it is invested at 10.5% compounded continuously?

   $A = P{e^{rt}}$

   $3 = 1{e^{.105t}}$

   $\ln 3 = \ln {e^{.105t}}$

   $\ln 3 = .105t$

   $\frac{{\ln 3}}{{.105}} = t$

   $10.46=t$

   It will take approximately 10.46 years for the initial investment to triple.

6. Radioactive Decay: A mathematical model for the decay of radioactive substances is given by $$Q = {Q_0}\;{e^{rt}}.$$ The continuous compound rate of decay of carbon-14 per year is $r = -0.0001238.$ How long will it take a certain amount of carbon-14 to decay to half the original amount?

   $\frac{1}{2} = 1{e^{ - 0.0001238t}}$

   $\ln .5 = \ln {e^{ - 0.0001238t}}$

   $\ln .5 = - 0.0001238t$

   $\frac{{\ln .5}}{{ - 0.000128}} = t$

   $t = 5598.93$

   It will take approximately 5598.93 years for the carbon-14 to decay to half the original amount.

7. The estimated resale value R (in dollars) of a company car after t years is given by: $$R(t) = 20000{(0.86)^t}.$$ What will be the resale value of the car after 2 years? How long will it take the car to depreciate to half the original value?

   $R(2) = 20,000{(0.86)^2} = \$ 14,792$

   The resale value of the car after two years will be $14.792.

   $\frac{{10,000}}{{20,000}} = \frac{{20,000{{(0.86)}^t}}}{{20,000}}$

   $.5 = {0.86^t}$

   $\ln .5 = \ln {0.86^t}$

   $\ln .5 = t\ln 0.86$

   $\frac{{\ln .5}}{{\ln 0.86}} = \frac{{t\ln 0.86}}{{\ln 0.86}}$

   $\frac{{\ln .5}}{{\ln 0.86}} = t$

   $t = 4.5957$

   It will take approximately 4.6 years for the car to depreciate to half its original value.

2.1 The Constant e and Natural Log Applications

Homework

Answer the following questions. Show all of your work. Round to two decimal places.

1. If you invested $1,000 in an account paying an annual percentage rate (quoted rate) of 2%, compounded continuously, how much would you have in your account at the end of

   1. 1 year

      $A = 1000{e^{.02(1)}} = 1020.20$

      At the end of one year, there will be $1020.20 in the account.

   2. 10 years

      $A = 1000{e^{.02(10)}} = 1221.40$

      At the end of ten years, there will be $1221.40 in the account.

   3. 20 years

      $A = 1000{e^{.02(20)}} = 1491.82$

      At the end of twenty years, there will be $1491.82 in the account.

   4. 50 years

      $A = 1000{e^{.02(50)}} = 2718.28$

      At the end of fifty years, there will be $2718.28 in the account.

2. A $1,000 investment is made in a trust fund at an annual percentage rate of 12%, compounded continuously. How long will it take the investment to

   1. Double

      $2000 = 1000{e^{0.12t}}$

      $2 = {e^{0.12t}}$

      $\ln 2 = \ln {e^{0.12t}}$

      $\ln 2 = 0.12t$

      $\frac{{\ln 2}}{{0.12}} = t$

      $t = 5.78$

      The investment will double in approximately 5.78 years.

   2. Triple

      $3000 = 1000{e^{0.12t}}\quad$

      $3 = {e^{0.12t}}$

      $\ln 3 = \ln {e^{0.12t}}$

      $\ln 3 = 0.12t$

      $\frac{{\ln 3}}{{0.12}} = t$

      $t = 9.16$

      The investment will triple in approximately 9.16 years.

3. If $500 is invested in an account which offers 0.75%, compounded continuously find:

   1. The amount A in the account after t years.

      $A = 500{e^{.0075t}}$

   2. Determine how much is in the account after 5 years, 10 years, 30 years, and 35 years.

      $A(5) = 500{e^{.0075(5)}}=519.11$

      After 5 years, $519.11 will be in the account.

      $A(10) = 500{e^{.0075(10)}}=538.94$

      After 10 years, $538.94 will be in the account.

      $A(30) = 500{e^{.0075(30)}}=626.16$

      After 30 years, $626.16 will be in the account.

      $A(35) = 500{e^{.0075(35)}}=650.09$

      After 35 years, $650.09 will be in the account.

   3. Determine how long it will take for the initial investment to double.

      $1000 = 500{e^{.0075t}}$

      $2 = {e^{.0075t}}$

      $\ln 2 = \ln {e^{.0075t}}$

      $\ln 2 = .0075t$

      $\frac{{\ln 2}}{{.0075}} = t$

      It will take approximately 92.42 years for the initial investment to double.

   4. Find and interpret the average rate of change of the amount in the account from the end of the fourth year (t=4) to the end of the fifth year (t=5).

      4th year $A(4) = 500{e^{.0075(4)}} = \$515.23$

      5th year $A(5) = 500{e^{.0075(5)}} = \$519.11$

      $\frac{A(5)-A(4)}{5-4}=\frac{519.11-515.23}{1}=3.88$

      The balance in the account is increasing by an average of $3.88 per year.

4. If $5000 is invested in an account which offers 2.125%, compounded continuously, find:

   1. The amount A in the account after t years.

      $A(t) = 5000{e^{.02125t}}$

   2. Determine how much is in the account after 5 years, 10 years, 30 years, and 35 years.

      $A(5) = 5000{e^{.02125(5)}} = 5560.50$

      After 5 years, $5560.50 will be in the account.

      $A(10) = 5000{e^{.02125(10)}} = 6183.83$

      After 10 years, $6183.83 will be in the account.

      $A(30) = 5000{e^{.02125(30)}} = 9458.73$

      After 30 years, $9458.73 will be in the account.

      $A(35) = 5000{e^{.02125(35)}} =10519.05$

      After 35 years, $10519.05 will be in the account.

   3. Determine how long it will take for the initial investment to double.

      $10,000 = 5000{e^{.02125t}}$

      $2 = {e^{.02125t}}$

      $\ln 2 = \ln {e^{.02125t}}$

      $\ln 2 = .02125t$

      $\frac{{\ln 2}}{{.02125}} = t$

      It will take approximately 32.62 years for the initial investment to double.

   4. Find and interpret the average rate of change of the amount in the account from the end of the fourth year (t=4) to the end of the fifth year (t=5).

      $A(4) = 5000{e^{.02125(4)}}$

      $A(4) = \$ 5443.59$

      $A(5) = 5000{e^{.02125(5)}}$

      $A(5) = \$ 5560.50$

      $\frac{A(5)-A(4)}{5-4}=\frac{\displaystyle5560.50-5443.59}{5-4}=\frac{\displaystyle116.91}1=116.91$

      The balance in the account is increasing by an average of $116.91 per year.

5. How much money needs to be invested now to obtain \$5000 in 10 years if the interest rate in a CD is 2.25%, compounded continuously?

   $A = P{e^{rt}}$

   $5000 = P{e^{0.0225(10)}}$

   $5000 = P{e^{0.225}}$

   $\frac{{5000}}{{{e^{0.225}}}} = \frac{{P{e^{0.225}}}}{{{e^{0.225}}}}$

   $\$ 3992.58 = P$

   \$3992.58 needs to be invested now, in order to have $5000 in 10 years.

6. A mathematical model for depreciation of a car is given by $A = P{(1-r)^t}$, where A is defined as the value of the car after t years, P is defined as the original value of the car, and r is the rate of depreciation per year. The cost of a new car is $32,000. It depreciates at a rate of 15% per year. This means that it loses 15% of its value each year.

   1. Find the formula that gives the value of the car in terms of time.

      $A = 32,000{\left( {1-0.15} \right)^t}$

      $A = 32,000{\left( {0.85} \right)^t}$

   2. Find the value of the car when it is four years old.

      $A = 32,000{\left( {.85} \right)^4}$

      $A = 16,704.20$

      The car is worth approximately $16,704.20 when it is 4 years old.

7. A mathematical model for depreciation of an ATV (all-terrain vehicle) is given by $A = P{(1-r)^t}$, where A is defined as the value of the vehicle after t years, P is defined as the original value of the vehicle, and r is the rate of depreciation per year. The cost of a new ATV (all-terrain vehicle) is \$7200. It depreciates at 18% per year.

   1. Find the formula that gives the value of the ATV in terms of time.

      $A = 7200{\left( {1-0.18} \right)^t}$

      $A = 7200{\left( {.82} \right)^t}$

   2. Find the value of the ATV when it is ten years old.

      $A = 7200{\left( {.82} \right)^{10}}$

      $A = 989.63$

      The value of the ATV when it is 10 years old will be $989.63.

8. Michigan's population is declining at a rate of 0.5% per year. In 2004, the state had a population of 10,112,620.

   1. Write a function to express this situation.

      $y = 10,112,620{\left( {.995} \right)^t}$

   2. If this rate continues, what will the population be in 2012?

      $y = 10,112,620{\left( {.995} \right)^8}$

      In 2012 the population of Michigan will be approximately 9,715,124 people.

   3. When will the population of Michigan reach 9,900,000?

      $9,900,000 = 10,112,620{\left( {.995} \right)^t}$

      $\frac{{9,900,000}}{{10,112,620}} = {.995^t}$

      $\ln (\frac{{9,900,000}}{{10,112,620}}) = \ln {.995^t}$

      $\ln (\frac{{9,900,000}}{{10,112,620}}) = t\;\ln .995$

      $\frac{{\ln (\frac{{9,900,000}}{{10,112,60}})}}{{\ln .995}} = t$

      $t = 4.24$ years

      The population of Michigan will be 9,900,000 people in March of 2008.

   4. What was the population in the year 2000, according to this model?

      $y = 10,112,620{\left( {.995} \right)^{ - 4}}$

      $y = 10,317,426.06$

      According to this model, the population of Michigan in 2000 was 10,317,426 people.

   https://sccmath.files.wordpress.com/2012/01/scc_open_source_intermediate_algebra.pdf

bellawerly.blogspot.com

Source: https://psccmath.github.io/math1830/u2s1.html

Share this post